Destructive in-order tree traversal

A few years ago, I decided to implement splaysort in my sorting algorithms library, cpp-sort. The algorithm turned out to be deceiptively simple from a high-level point of view:

1. Insert all elements to sort into a splay tree (a kind of self-balancing binary search tree).
2. Perform in-order traversal on the tree to move elements back to the original collection in sorted order.

It is basically just a tree sort, which benefits from the ability of splay trees to gracefully adapt to the existing order in a sequence. As a matter of fact, the splay tree itself looks no different from any other binary search tree:

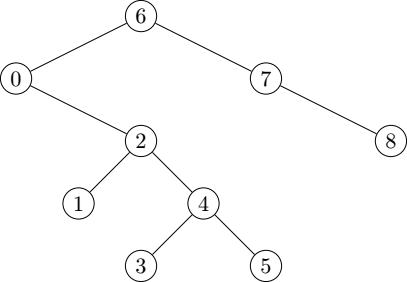
This article is not really about splaysort, nor about tree sorts: it is about in-order traversal of binary search trees.

In-order traversal in its simplest form

Visiting a binary search tree in-order is most easily explained through the recursive definition of the algorithm:

1. Recursively visit the node’s left child if any.
2. Visit the current node (in our case, move the value back to the original collection).
3. Recursively visit the node’s right child if any.

It is perhaps even clearer when compared to pre-order and post-order traversals:

pre-order	in-order	post-order
func pre-order(node): visit(node) pre-order(left-child) pre-order(right-child) }	func in-order(node): in-order(left-child) visit(node) in-order(right-child) }	func post-order(node): post-order(left-child) post-order(right-child) visit(node) }

If we start such traversal with the root node, we can move all values back to the original collection in sorted order thanks to the fundamental property of binary search trees: left children have a smaller value than that of the current node, right children have a greater value.

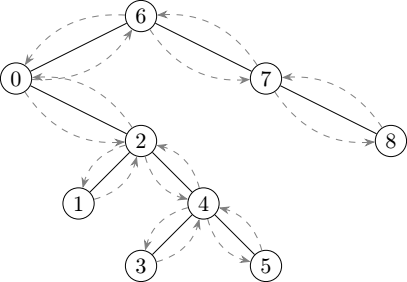
The following illustration gives an idea of the order in which the nodes are walked through during an in-order traversal:

C++ recursive implementation

We’re gonna use the following node type to implement in-order traversal in C++:

template<std::movable T>
struct node
{
    T value;
    node* parent;
    node* left;
    node* right;
};

The recursive traversal function moving values out of our tree and into an output iterator looks like this:

template<std::movable T, std::output_iterator Iterator>
void move_to(node<T>* node, Iterator& out)
{
    if (node == nullptr) return;
    move_to(node->left, out);
    *out++ = std::move(node->value);
    move_to(node->right, out);
}

So far we got a beautifully simple algorithm. Call it on the root and it moves your whole tree away, which is exacty what we want.

C++ iterative implementation

Technically the recursive version of in-order traversal is enough for our use case: we are using a splay tree, which is self-balancing, so its depth should never exceed \(O(log n)\). Non-balancing trees can become degenerate, forcing one to dive down through \(O(n)\) layers, potentially blowing the stack, though that simply can’t happen to us. I could have stopped there but I wanted to implement an iterative tree traversal, and it turns out that there are lots of different ways to do that. Many of those either use a stack of nodes to mimick recursion, or use more involved alternatives such as Morris threaded binary tree in-order traversal.

As much as possible I didn’t want to allocate additional memory, and threading a binary seemed complicated at the time. Fortunately I had a considerable advantage up my sleeve: parent pointers! Splaying operations often involve following parent nodes, which makes such a traversal much easier. Nevertheless I was still a lazy bum, and instead of trying to come up with a smart solution, I did what most millenials do when faced with such an exciting challenge: copy-pasting some code from StackOverflow.

void in_order_traversal_iterative_with_parent(node* root) {
node* current = root;
node* previous = NULL;

while (current) {
    if (previous == current->parent) { // Traversing down the tree.
        previous = current;
        if (current->left) {
            current = current->left;
        } else {
            cout << ' ' << current->data;
            if (current->right)
                current = current->right;
            else
                current = current->parent;
        }
    } else if (previous == current->left) { // Traversing up the tree from the left.
        previous = current;
        cout << ' ' << current->data;
        if (current->right)
            current = current->right;
        else
            current = current->parent;
    } else if (previous == current->right) { // Traversing up the tree from the right.
        previous = current;
        current = current->parent;
    }
}

cout << endl;
}

That piece of C++ code is the work of StackOverflow user @OmarOthman, based on a previous answer by @svick. The algorithm revolves around the fact that knowing where we come from is enough to know where we need to go next:

1. If we come from a parent node, it is our first time seeing that node, we go left if possible.
2. If we come from a left child node, we visit the current node, then our next target is the right node.
3. If we come from a right node, all we can do is bubble up to the parent node.

In all of those steps, if our next target is null, we behave as if we were in the subsequent state. Interestingly enough, that “fallback behaviour” shows better with a few labels and goto:

template<std::movable T, std::output_iterator Iterator>
void move_to_1(node<T>* root, Iterator out)
{
    node<T>* current = root;
    node<T>* previous = nullptr;

    while (current) {
        if (previous == current->parent) {
            goto from_parent;
        } else if (previous == current->left) {
            goto from_left;
        } else if (previous == current->right) {
            goto from_right;
        }
        
        from_parent:
            if (current->left) {
                previous = std::exchange(current, current->left);
                continue;
            }
        from_left:
            *out++ = std::move(current->value);
            if (current->right) {
                previous = std::exchange(current, current->right);
                continue;
            }
        from_right:
            previous = std::exchange(current, current->parent);
    }
}

Given a tree with \(n\) nodes, this algorithm’s main loop is executed \(2n\) times:

• Every node is considered once in the initial “going down” phase, which leads to \(n\) executions of the loop.
• When “going up” after visitation, every node picks its parent as the next node, which gives another \(n\) executions of the loop.

This number of loops is independent of the data in the tree, and of whether the tree is balanced or not. This implementation actually reflects what happens in the recursive one, where every function call has control when first reached, then again after the recursive calls return to it. And that is no surprise: the labelled sections in this sequential implementation correspond to where control would resume in the recursive implementation after a recursive call.

The question is now: can we do better without introducing additional pointers, recursion, or stack space?

Grandma’s delicious goto soup

This article is somehow already going places it was never supposed to, so I’m just gonna double down on the goto soup and have fun trying to iteratively rewrite and prune parts of it. Let’s start right away with a few observations:

1. The first previous == current->parent check is redundant: if the two following checks fail, then we naturally reach from_parent:.
2. The very first loop satisfies the from_parent criterion, we can jump there directly.
3. When visiting a left child, the first thing we want to do is to recursively find another left child. We can skip a few conditions by introducing a tight loop.
4. When visiting a right child, we know that we will be coming from the parent node in the following loop iteration, we can jump there directly.

Putting it all together, we get the following modified version of the algorithm:

template<std::movable T, std::output_iterator Iterator>
void move_to_2(node<T>* root, Iterator out)
{
    node<T>* current = root;
    node<T>* previous = nullptr;

    goto from_parent; // (2)
    while (current) {
        // (1) removed (previous == current->parent) condition
        if (previous == current->left) {
            goto from_left;
        } else if (previous == current->right) {
            goto from_right;
        }
        
        from_parent:
            while (current->left) { // (3)
                previous = std::exchange(current, current->left); // (A)
            }
        from_left:
            *out++ = std::move(current->value);
            if (current->right) {
                previous = std::exchange(current, current->right); // (B)
                goto from_parent; // (4)
            }
        from_right:
            previous = std::exchange(current, current->parent);
    }
}

All that tinkering changes nothing to the number of nodes that have to be considered at any given moment by the algorithm, which remains \(2n\). However it effectively reuses knowledge about the algorithm flow to reduce the number of conditions performed during a traversal. Amazingly enough, experimental data shows that the number of conditions seems independent of the node values, with \(6n\) conditions for the previous version and \(4n\) for the new one.

An additional optimization we can perform here is avoiding to the assignment to previous when we know that the variable won’t be used before being overwritten again (marks A and B in the code snippet above). This improvement however is unlikely to make the algorithm much faster: it saves a few pointers copies, but speed is likely dominated by branching and pointer chasing.

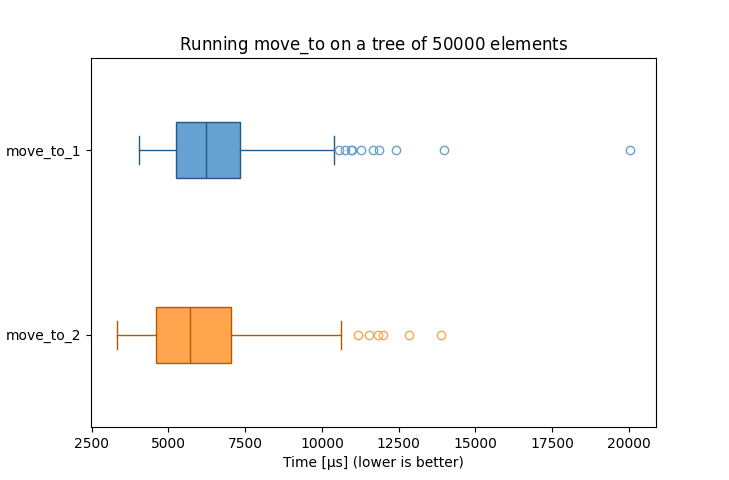
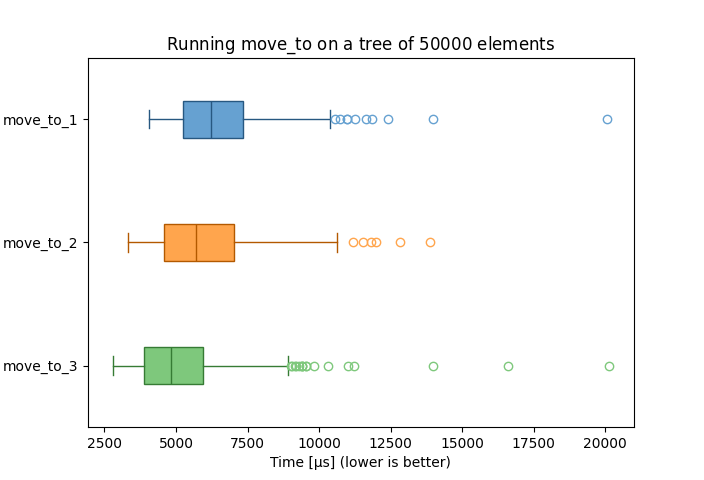
The boxplot above was generated by running move_to_1 and move_to_2 (including the latest proposed optimization) as part of splaysort, which theoretically means that the move-from trees are all balanced. As such there should be a fairly high rate of branch misprediction. It is the result of running 10k samples over collections of 50k integers, with the same PRNG seed used for both algorithms. The program was compiled with MinGW-w64 g++ 14.1.0 on an i7-4710MQ with options -std=c++23 -O2.

The optimized version seems overall slightly faster than the original one. I tried to rerun the benchmark several times and got varying results, though the conclusion generally remains the same.

Destructive iterative traversal

As you can guess, I didn’t start a blog post just to present how to shuffle around someone else’s code, as fun as it may be. What comes next is the core idea behind this article: taking advantage of the fact that we don’t need the tree anymore after the traversal to improve it. We are gonna rewrite pointers in an effort to reduce pointer chasing, in a way that makes links between nodes inconsistent.

Anyway, let’s first go back to our original illustration of in-order tree visitation and annotate it with a few colours:

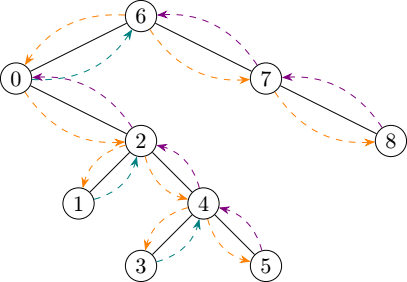
I used three colours in that diagram to differentiate between three kinds of moves we perform during a traversal:

• Orange: going down.
• Teal: going up to visit a node.
• Violet: going up to a node that has already been visited.

There’s no avoiding the first two categories of moves, but I would very much like to get rid of the third one. After all it’s fairly boring to go back up to a node we have already visited, only to immediately leave it to go up again.

Sooooo, let’s just do that, shall we? When moving down to the right child of a given node, maybe we can just reassign the node’s parent to its grandparent?

if (current->right) {
    previous = std::exchange(current, current->right);
    current->parent = previous->parent; // NEW
    goto from_parent;
}

Does it work? Well, no it doesn’t: overwriting the parent link unsurprisingly breaks the condition that relies on it:

if (previous == current->left) {
    goto from_left;
} else {
    goto from_right;
}

However there is a silver lining there: we don’t actually need that condition anymore! To understand why, let’s look at what our optimized traversal looks like:

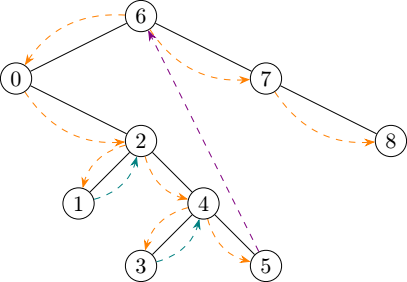
In this optimized traversal, whenever we come back from a child node, we do it “as if” we came from a left node: we visit the current node, then check whether there is a right child to visit, then a parent node. Since this entirely erases the difference between from_left: and from_right:, we can replace both with just from_left:, rename it into from_child and get rid the problematic condition altogether:

template<std::movable T, std::output_iterator Iterator>
void move_to_3(node<T>* root, Iterator out)
{
    node<T>* current = root;
    node<T>* previous = nullptr;

    goto from_parent;
    while (current) {
        goto from_child;
        
        from_parent:
            while (current->left) {
                current = current->left;
            }
        from_child:
            *out++ = std::move(current->value);
            if (current->right) {
                previous = std::exchange(current, current->right);
                current->parent = previous->parent; // Overwrite parent link
                goto from_parent;
            }
            previous = std::exchange(current, current->parent);
    }
}

Does it work now? Yes it does! However the looping structure mixed with goto is a bit awkward, and the previous variable is now only needed to rewrite the parent link. Let’s clean all that up a bit:

template<std::movable T, std::output_iterator Iterator>
void move_to_3(node<T>* root, Iterator out)
{
    node<T>* current = root;

    from_parent:
        while (current->left) {
            current = current->left;
        }
    from_child:
        *out++ = std::move(current->value);
        if (current->right) {
            auto previous = std::exchange(current, current->right);
            current->parent = previous->parent; // Overwrite parent link
            goto from_parent;
        }
        current = current->parent;
        if (current) {
            goto from_child;
        }
}

How does it perform? Experimental evidence shows that:

• With a degenerate tree where every node is a left node, the algorithm still has to take decisions for \(2n\) nodes.
• With a degenerate tree where every node is a right node, the algorithm only takes decisions for \(n\) nodes and immediately jumps back to the root and finishes.
• In the case of a well-balanced tree such as a splay tree, the algorithm takes decisions for around \(\frac{3}{2}n\) nodes.

The number of comparisons performed by the optimized algorithm is not deterministic anymore, but similarly falls down to around \(\frac{5}{2}n\), which is an improvement over the previous \(4n\).

If you remember the previous section of this article, I suspected pointer chasing to slow down the algorithm. The parent node rewrite optimization effectively allows us to overwrite parent pointers without having to follow (dereference) them, which means that we should be able to notice a difference in speed.

Looks like a success. Taking advantage of the fact that we won’t need our tree after the traversal effectively allowed us to intrusively modify it on the fly and to speed things up.

Note: I ran the same benchmark several times with similar results; only the number of outliers in the boxplots changes every now and then. I decided to keep results where the few outliers don’t dwarf the the boxplots entirely (I got one or two reaching 100~150µs), as I’d rather keep readable results, and external factors were likely to blame for those.

Bonus chatter: traversing the tree again

But Morwenn, you said that you can’t traverse the tree anymore once we are done. I think it’s still fine?

Thanks for asking! The truth is I lied.

Or to be exact, the impact is much tamer than I thought it would be when I started writing this article:

• If not for the std::move part, we can run as many such iterative traversals as we want. It’s fine.
• We can also perform recursive traversals on that tree all the same, they don’t need that parent node.
• More generally: as long as we don’t need the parent node for anything else, everything still works fine.

Even better: we can actually restore the correct value of the parent nodes if needed. All we need to do is to run a non-destructive traversal algorithm (like move_to_2) and add current->parent = previous; when visiting a right child node.