In a previous article, I introduced a new measure of disorder that I called \(Amp\) and attempted to determine whether it is a measure of presortedness (it is not). In this short note, I am going to demonstrate another property of \(Amp\): its symmetry over the input sequence. That is:

\[Amp(Reversed(X)) = Amp(X)\]

In this article, we are using the following definition for \(Amp\), which takes into account elements that compare equal (see previous article for what the individual terms mean):

\[Amp(X) = \lvert X \rvert - PTP(X) - N_{eq}(X) - 1\]

We already saw in the previous article that \(Amp(X) = 0\) when \(X\) is a sorted sequence, but also when \(X\) it is a reverse-sorted sequence, which is a special case of that property. We can as easily find examples with much more random sequences, let’s take one from the original article:

\[X = \langle 4, 6, 6, 6, 7, 8, 6, 4, 3, 2, 5, 6, 1, 2, 7, 7, 5, 6, 8, 11, 11, 11, 9, 7, 8, 6 \rangle\]
  • ‎\(Amp(X) = \lvert X \rvert - PTP(X) - N_{eq}(X) - 1 = 26 - 5 - 5 - 1 = 15\)
  • ‎\(Amp(Reversed(X)) = \lvert Reversed(X) \rvert - PTP(Reversed(X)) - N_{eq}(Reversed(X)) - 1 = 26 - 5 - 5 - 1 = 15\)

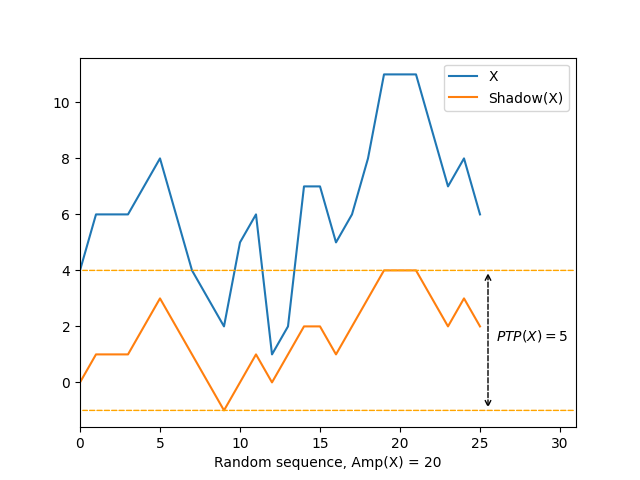
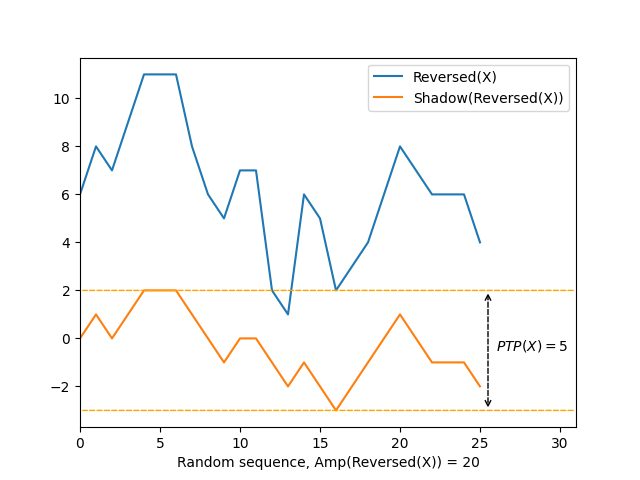
Line graph of a sequence of integers and its shadow, with the peak-to-peak amplitude illustrated Same as above, with the same sequence of integers reversed

The first striking observation is the sheer amount of symmetry in the different elements that contribute to \(Amp\):

  • ‎\(\lvert Reversed(X) \rvert = \lvert X \rvert\)
  • ‎\(PTP(Reversed(X)) = PTP(X)\)
  • ‎\(N_{eq}(Reversed(X)) = N_{eq}(X)\)

The size of a reversed sequence being equal to the size of the original sequence is trivially true, and it makes sense that the number of elements that compare equivalent is the same, no matter the direction in which we traverse a sequence. I don’t think those need to be demonstrated any further, which leaves one thing to prove: the symmetry of \(PTP(Reversed(X)) = PTP(X)\).

The line graph above gives an intuitive explanation: the peak-to-peak amplitude of the shadow of the reversed sequence is the same as that of the sequence because the shadow of the reversed sequence is a reversal of the shadow of the sequence, shifted along the vertical axis by some constant value. More formally, we need to prove the following conjecture (assuming 1-based indexing):

\[Shadow_i(Reversed(X)) = Shadow_{\lvert X \rvert - i + 1}(X) + V\]

Where \(V = -Shadow_{\lvert X \rvert}(X)\) is the aforementioned shift along the vertical axis (also conjectured from the line graph).

We start by restating the definition of \(Shadow(X)\): it is the prefix sum of the pairwise order of the elements of \(X\) (called \(Order(X)\) below), which is itself a sequence of \(\lvert X \rvert\) elements taking the values \(-1\), \(0\) or \(1\) (always prefixed with a single \(0\)).

Pairwise order shadow of a sequence of elements: sequence 3, 4, 6, 6, 6, 7, 8, 6, 4 and the pairwise order shadow 1, 2, 2, 2, 3, 3, 2, 1

By definition, the ith element of \(Shadow(X)\) is the sum of elements \(1\) to \(i\) (inclusive) of the pairwise order of \(X\):

\[Shadow_i(X) = \sum_{k=1}^i Order_k(X)\]

We prove the conjecture with the following reasoning:

\[\begin{aligned} Shadow_i(Reversed(X)) & = \sum_{k=1}^i Order_k(Reversed(X))\\ & = \sum_{k=\lvert X \rvert-i+2}^n -1 * Order_k(X) & \text{ (1) }\\ & = -1 * \sum_{k=\lvert X \rvert-i+2}^n Order_k(X)\\ & = -1 * (\sum_{k=1}^{\lvert X \rvert} Order_k(X) - \sum_{k=1}^{\lvert X \rvert-i+1} Order_k(X)) & \text{ (2) }\\ & = \sum_{k=1}^{\lvert X \rvert-i+1} Order_k(X) - \sum_{k=1}^{\lvert X \rvert} Order_k(X)\\ & = Shadow_{\lvert X \rvert-i+1}(X) - Shadow_{\lvert X \rvert}(X) \end{aligned}\]

\((1)\) follows from the definition of the pairwise order: it is a collection made of a single \(0\) element followed by the pairwise comparison pairs of adjacent elements according to the following comparison function:

\[comp(x, y)= \begin{cases} 1 & \text{ if } x \lt y\\ -1 & \text{ if } x \gt y\\ 0 & \text{otherwise} \end{cases}\]

When traversing the collection in reverse order, we end up performing the same comparisons starting from the end of the sequence, with the order of its parameters flipped. It is trivial to see that \(comp(y, x) = -comp(x, y)\), which gives us that the first \(n\) elements of the pairwise order of a reversed sequence correspond to \(0\) followed by the last \(n-1\) elements of the pairwise order of the original sequence, reversed and negated:

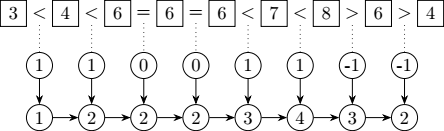
Example, with arbitrary emphasis on the first three elements of a sequence, and the corresponding pairwise order:

Index 1 2 3 4 5 6 7 8 9
\(X\) 3 4 6 6 6 7 8 6 4
\(Order(X)\) 0 1 1 0 0 1 1 -1 -1
\(Reversed(X)\) 4 6 8 7 6 6 6 4 3
\(Order(Reversed(X))\) 0 1 1 -1 -1 0 0 -1 -1

\((2)\) is the simple observation that the sum of a subsequence equals the sum of the whole sequence minus the sum of the rest of the sequence.

Q.E.D.

Back to our original conjecture, we can conclude as follows:

\[\begin{aligned} PTP(Reversed(X)) & = \max Shadow(Reversed(X)) - \min Shadow(Reversed(X))\\ & = \max (Shadow(X) + V) - \min (Shadow(X) + V)\\ & = \max Shadow(X) - \min Shadow(X)\\ & = PTP(X) \end{aligned}\]

And that’s it, that’s enough to show that \(Amp(Reversed(X)) = Amp(X)\).