Introduction

This article is just a quick note about an observation I made today, so I intend to keep it short. First of all, let’s go back to the definition of what is a measure of presortedness:

Given two sequences \(X\) and \(Y\) of distinct elements, a measure of presortedness \(M\) is a non-negative integer function that satisfies the following properties:

  1. If \(X\) is sorted, then \(M(X) = 0\)
  2. If \(X\) and \(Y\) are order isomorphic, then \(M(X) = M(Y)\)
  3. If \(Y\) is a subsequence of \(X\), then \(M(Y) ≤ M(X)\)
  4. If \(X \le Y\), then \(M(XY) ≤ M(X) + M(Y)\)
  5. ‎\(M(\langle e \rangle X) \le \lvert X \rvert + M(X)\) for every element \(e\) of the domain

Those five axioms were proposed by Heiki Mannila in his paper 1985 paper Measures of presortedness and optimal sorting algorithms. In the same paper, he discusses a few existing “natural measures of disorder”, including \(Exc\) which is defined as the smallest number of exchanges of arbitrary elements needed to bring \(X\) into ascending order.

Additionally he adds a method to compute \(Exc\):

\(exc(X) = n -\) the number of cycles in the permutation of \(\{1 , n\}\) corresponding to \(X\).

Let’s take for example the sequence \(\langle 2, 4, 0, 6, 3, 1, 5 \rangle\). It contains the following cycles:

  • ‎\(\langle 2, 0 \rangle\)
  • ‎\(\langle 4, 3, 6, 5, 1 \rangle\)

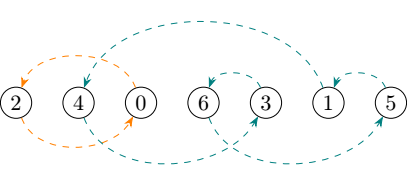
As a result, we get \(Exc(X) = \lvert X \rvert - 2 = 5\).

Mannila then discusses the inuition behind each of the five axioms he picked, and follows with this claim:

The measures presented in Section II-A are easily seen to satisfy properties 1)-5), once they have been scaled to have value 0 for a sorted list.

The mention of scaling only concerns \(Runs\), another measure of presortedness, and we can ignore it for \(Exc\) which already returns 0 for a sorted list. \(Exc\) is among the measures presented in section II-A of the paper, which means that it is assumed to satisfy the five axioms by the author.

Finding a counterexample with property-based testing

I have shipped an implementation of \(Exc\) along with some tests in my library cpp-sort for most of a decade. Those tests however were fairly brittle, so I recently decided to make them more robust with the power of RapidCheck and property-based tesding. Mannila’s five axioms, being the very foundation of the formal concept of a measure of presortedness, were a natural target for property tests.

\(Exc\) gave me some difficulties over the years, and this time was no different. The main culprit was equal elements in the sequence: the formal definition only cares about distinct elements, but I try to extend my implementation to support equal elements when possible. After failing to find a satisfying solution for \(Exc\), I discovered that the problem is actually NP-hard in the presence of equivalent elements, a result that was proved by Amir and al in One the Cost of Interchange Rearrangement in Strings.

Admitting my defeat, I added a note about equal elements to the documentation, then settled on testing Mannila’s axioms on distinct elements. That’s when RapidCheck gave me a failing result for axiom 3 (a subsequence shall contain no more disorder than the whole sequence) with the following sequence:

\[X = \langle 2464, 2497, 2387, 0, 409 \rangle\]

I had already tested the second axiom by then (order isomorphism), so I knew I could use simpler values and get the same result:

\[X = \langle 3, 4, 2, 0, 1 \rangle\]

This sequence has three cycles: \(\langle 3, 0 \rangle\), \(\langle 4, 1 \rangle\) and \(\langle 2 \rangle\), which means that \(Exc(X) = \lvert X \rvert - 3 = 2\).

Now remove the \(0\) from \(X\) and you get the following subsequence:

\[Y = \langle 3, 4, 2, 1 \rangle\]

This subsequence has a single cycle \(\langle 3, 2, 4, 1 \rangle\), which gives \(Exc(Y) = \lvert Y \rvert - 1 = 3\). It indeed seems like it cannot be sorted with fewer than three exchanges.

This counterexample proves that there exists sequences for which \(Exc(subsequence(X)) \gt Exc(X)\), which violates Mannila’s third axiom, and that \(Exc\) is not a well-behaved measure of presortedness.

Double-checking the literature

\(Exc\) is likely one of the oldest metrics proposed to evaluate disorder in a sequence, and as such appears in most the literature about measures of presortedness. I wanted to make sure that I had not missed anything, so I performed the following checks:

  • Mannila never proves that \(Exc\) is a measure of presortedness, he only claims it.
  • I could not find any counterexample in the subsequent literature, nor any other claim that \(Exc\) was not well-behaved.
  • Mannila does not specify that “subsequence” can be made of non-consecutive elements in axiom 3, though we can derive that from the following bits:
    • He describes runs as “ascending substrings”,
    • He uses “subsequence” in “longest ascending subsequence”, which does not have to be made of consecutive elements.
    • Other authors, some who had private discussions with Mannila, clearly differentiate “subsequence” from “consecutive subsequence” and make it clear in their definitions that axiom 3 is also about non-consecutive elements.
    • All other proposed measures of presortedness seem to actually satisfy axiom 3 when interpreting “subsequence” as non-consecutive elements, as far as I could test.
    • Authors who propose new measures of presortedness and prove that they satisfy axiom 3 also interpret “subsequence” as elements that don’t have to be consecutive.
  • Estivill-Castro and Wood mention several measures of disorder from the literature (for example \(Enc\)) and how they don’t satisfy some axioms, but seem to never question \(Exc\).

I might have missed something, don’t hesitate to reach out to me if you find an error or have more information. \(Exc\) corresponds to a fairly general problem in computer science and likely appears under other names in another branch of the literature, so that result might already be known, yet remain unknown to the literature specific to sorting and presortedness.